今日学習ボランティアとしておじゃました2年生の授業は、算数の《長さを計算する》でした。
㎝や㎜の単位のついている長さを足したり引いたり。
㎝や㎜を習いはじめたばかりの子ども達とかかわった経験をもとに、長さを計算するときのポイントをまとめてみました。
これまでの復習「3㎝と8㎜はどちらが長い?」
たしか㎝と㎜の勉強が始まったのが先週。
子ども達にとっては、㎝と㎜はまだまだ難しそうです。
先生の適切な介入がなければ、あやうく「8㎜の方が長い」になりそうでした。
3と8だけ比べれば、8の方が大きい。
でも、3についているのは㎝だよ。
8についているのは㎜だよ。
3㎝を㎜に変身させると「30㎜」。
㎜どうしになったから、数字をそのまま比べていいんだよね。
30>8
子ども達は、1週間前にものさしを使いはじめたばかりです。
yukkuritokomi.com
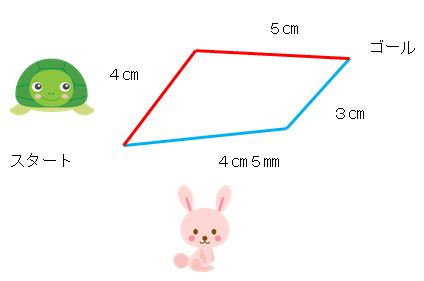
今日の授業は「かめとウサギのゴールまでの長さ」
ウサギは青い道をいきました。
それぞれのゴールまでの長さを計算してください。

「かめとウサギ」の童話をみな知っているせいか、クラス全員が黒板の図に見入って集中しています。
問題の導入部分で「かめとウサギ」が使われていることは、子ども達に問題の意図を理解させるのにおどろくほど効果的でした。
本題に入る手前とはいえ、この「全員集中」は見ていてちょっとした感動ものです。
こんなふうに、新しい勉強の導入部分で、子ども達の経験や興味のあることをうまく織り交ぜることは大切なことだと思いました。
かめの道は曲がっています。

でもこうすると、長さをはかることができるよ。
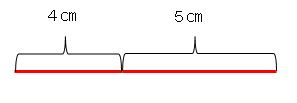
4㎝+5㎝=▢
両方とも㎝だから、そのまま4と5をたしていいよね。
4+5=9
答えは9㎝
しかし、今日のねらいは、ウサギの道のほうです。

これをまっすぐにすると。
式はどうなるのかな。
それから?
そして?
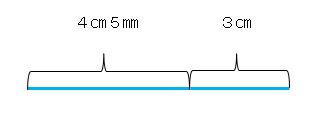
4+3=7
単位をつけて、7㎝。
5㎜をたして、7㎝5㎜。
ポイント
㎝どうし、㎜どうしでたす
4㎝5㎜+3㎝
「㎝どうしでたす」まではわかるのですが、そのあと5㎜をどうするのかがわからないようです。
つまり、4㎝+3㎝=7㎝
そのあと、7㎝+5㎜=12㎝となってしまうのです。
3㎝には㎜の数字がくっついていない。
だから5㎜にたすべき相手はいない。
5㎜はただそのまま、7㎝にくっつけるだけ。
答えは7㎝5㎜。
10㎜の真ん中には5㎜のメモリがある
子ども達にとって、数をかぞえる時に、1つずつ数えていくことは安心でき、全体数を実感しやすい方法です。
しかし、時間がかかり間違えやすい。
だから段々に、5ずつ(5、10、15)や10ずつ(10,20,30)で数え、残りの端数だけを1つずつ数えられるようになれたら。
そして、単元が進んできた今、「1つずつ数え」の限界を感じはじめています。
なぜなら、この「1つずつ数え」が㎜単位には通用しないからです。
どういうことかというと、ものさしのメモリが小さすぎて1つずつ数えられないのです。
自分の指先よりも小さい幅を、1つずつ指先でおうのはかなり困難です。
これまでは、どんなに非効率でも両指を使い、かぞえ棒をあるだけ使い数えてきましたが、この「戦法」はここから先は難しそうです。
そこで、どうしても10㎜の真ん中にあり、少し頭の出ている5㎜を目安にせざるをえません。

たとえば。
5㎜を中心に、2㎜少ないから3㎜である
⇒ 「5㎜-2㎜=3㎜」
5㎜を中心に、2㎜多いから7㎜である
⇒ 「5㎜+2㎜=7㎜」
「5のともだち」「10のともだち」の復習
そして、cmやmmの出番となってもベースになっているのは「5のともだち」と「10のともだち」。
「九九」が始まる前に、マスターできるといいのですが。
1と4
2と3
◎10のともだち
1と9
2と8
3と7
4と6
5と5
クラスには、「1」と言っても「9」とすぐに言えない子どもさんもいます。
45分間の授業にはすすむべきスピードがあり、授業の中で「ともだち」を何度も復習することはありません。
家に帰って、反復練習1日10分!
今ならまだぜんぜん間に合うと思うのですが。
