今日、学習ボランティアとしておじゃました小学6年生の授業は、算数の「場合の数の調べかた」でした。
場合の数の問題を解くためのポイントは、ズバリ次の1点につきると思います。
その問題を解くために必要な図や表をイメージできるかどうか
具体的な問題でみていきましょう。
クラスの人数は40人。トマトの好きな人は25人、ピーマンの好きな人は12人。両方好きな人は8人。両方嫌いな人は何人ですか。
まったくわからない場合
ポイント1:問題を表にできるか
まずやることは、この文章を図にしてみることです。
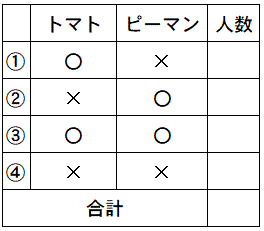
①トマトは好きでピーマンは嫌いな人数
②トマトは嫌いでピーマンは好きな人数
③両方好きな人数
④両方きらいな人数
文章から、仕分けする人数は4種類あることを読み取る必要があります。
ポイント2:数がわかった欄からうめていく
③の両方好きな人は8人。
クラスの人数は40人。
この2つは問題に書いてあるそのままの数字を入れることができます。
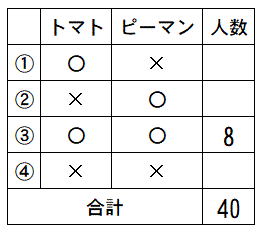
続いて、トマトが好きでピーマンがきらいな人は?
問題文からわかるのは、トマトが好きな人は25人。
トマトとピーマンの両方好きな人は8人。
これを図にしてみると次のようになります。
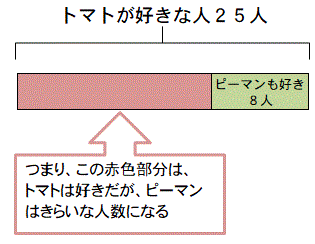
トマトは好きでピーマンがきらいな人は。
25-8=17人となります。
①の人数がわかりました。
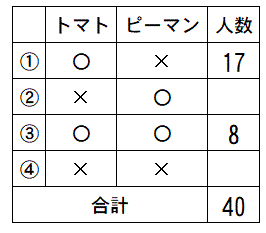
次は、トマトはきらいでピーマンが好きな人です。
問題文からわかるのは、ピーマンが好きな人は12人。
トマトとピーマンの両方好きな人は8人。
これを図にしてみると次のようになります。
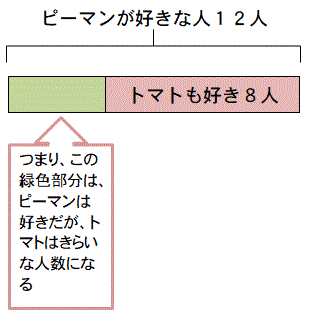
トマトが嫌いでピーマンが好きな人は。
12-8=4人となります。
②の人数がわかりました。
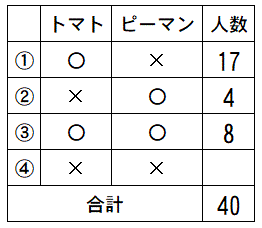
ここまで表がうまると、④の人数を求めるのは簡単です。
④=40-(17+4+8)=11人
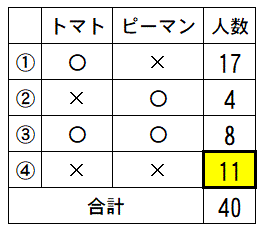
トマトとピーマンの両方嫌いな人は11人ということになります。
簡単な図や表で理解できる場合
仕分けする人数が4種類に分かれることが理解できる子どは、もっと簡単な図や表でいけます。
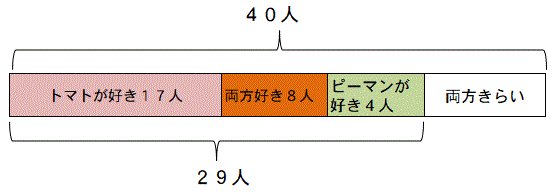
文章から読み取れる数字を入れていきます。
<図>
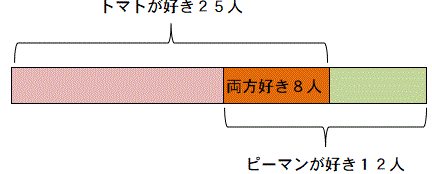
片方だけが好きな人数を出します。
トマトだけ好き=25―8=17人
ピーマンだけ好き=12-8=4人
全員で人数は40人です。
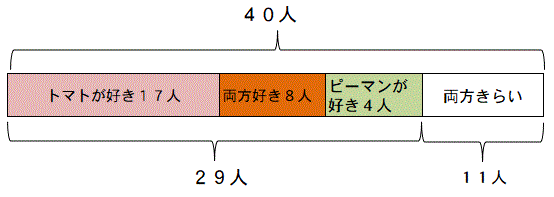
両方きらいな人=40-29=11人
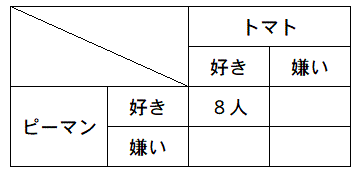
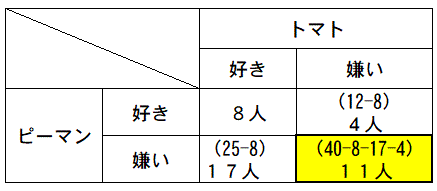
<表>
両方好きな人は8人です。
トマトだけ好きな人=25-8=17人です。
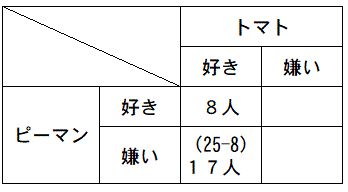
ピーマンだけ好きな人=12-8=4人です。

4マスの合計は40人のため、両方嫌いな人は。
40-(8+17+4)=11人
まとめ
(文章)問題を図や表で表せないということは、何を仕分けていいのかがまだつかめていないということになります。
小学校で出る問題はパターンが多くないため、トマトをいちごに置き換えて図や表がさっと書けるようになるまで練習が必要になってきます。
他にも学習ボランティアに関する記事はこちらからどうぞ