今日、学習ボランティアとしておじゃました小学2年生の授業は、「2ケタ+1ケタ」のたし算でした。
「23+ 7」のように、2ケタの1の位の数字と1ケタの数字をたすと、ぴった10になります。
感覚的にとらえやすいと思うのですが、それでも計算ができなくて困っている子どももいます。
つまづいている子どもが、ピンときたり理解ができるようになった教えかたや声がけをまとめてみました。
「10の組み合わせ」
まずは、「10の組み合わせ」の復習です。
「1」と言われたら「9」。
「2」であれば「8」。
今日の授業には、この「10の組み合わせ」を理解していることが必要です。
1-9
2-8
3ー7
4-6
5-5
逆もあります。
6-4
7-3
8ー2
9-1
2ケタ+1ケタの計算方法
今日の問題です。
- まず、かぞえ棒をつかって、23を「10のかたまり」と「バラ」にわけます。
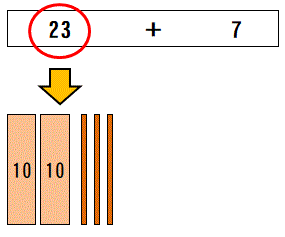
「10のかたまり」2つと(「バラ」が)3になります。 - この3と7をたします。

3 + 7 = 10になります。 - 23の20と、この10をたします。

20 + 10 = 30(答え)
具体的な声がけの方法
しかし、この説明を1回聞いただけでは、のみこめない子どももいます。
配られたプリント問題に手がつけられずに困っています。
①18 + 2
②11 + 9
③14 + 6
④13 + 7
⑤26 + 4
こんなときは、
「①番からやっていくよ。」
どの問題をやろうとしているのか意識づけ
「問題を読んでみて。」
子どもに読ませます
「18の8と2をたすといくつになる?」
(答え:10)
まず、どことどこをたすのか教えます
「次に、その10と18の10をたすと?」
(答え:20)
次にやることを教えます
「そうだよ。OK!」
答えが出せたら、「OK!」「正解!」「すごい!」を連発
残りの問題も同じように繰り返します。
間をあけず繰り返すことで、ようやく2ケタの数字を「10のかたまり」と「残りのバラ」に分けることがしみこんでいくようです。
ポイント
ポイントは2つ
- 「10の組み合わせ」がすっと言えるか
- 2ケタの数字を「10のかたまり」と「バラ」にわけられるか
10より大きい数になってくると、かぞえ棒や指をつかって数えるのは時間がかかり、数えまちがいもおきやすくなります。
数字を「10の組み合わせ」と「10のかたまり」でとらえることは、この先の算数の学習の土台となり、とても大切なことです。